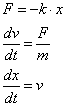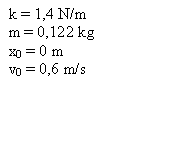Materiale

Valg af værktøj

 

4. Krus ophængt i lang elastik


I det følgende skal du lave en model for et krus ophængt i en meget lang elastik.

Elastikken bestod af et stort antal husholdningselastikker, der var bundet sammen til én lang elastik.

Der er lavet følgende målinger:

Massen af kruset m:     m = 0,122 kg

Så længe forlængelsen af elastikken ikke er for stor sammenlignet med elastikkens længde, er Hooks Lov en god model for elastikken (, hvor k er fjederkonstanten).

Kruset blev hængt op i elastikken, og forlængelsen af elastikken ()blev bestemt til 0,85 m (forlængelsen af elastikken er bestemt med nogen usikkerhed).

  1. Bestem fjederkonstanten for elastikken.


    (Kontrol: k = 1,4 N/m)


Kruset i elastik blev hængt op i loftet og sat til at svinge omkring ligevægtsstillingen.

Målingerne blev lavet med SW udstyr ("Ekkoloddet").

Du kan finde målingerne i Excel-regnearket Fjeder, desuden som PowerSim dokumentet fjeder.

Gem ovenstående to filer i én mappe på din PC. Åbn PowerSim-dokumentet, og start en simulering. Du skal nu kunne se en graf over målingerne.

For at kunne sammenligne målinger og model skal du opbygge modellen i ovenstående PowerSim-dokumentet.

Nedenfor ses den simple model for ovenstående forsøg:

(Hook's lov, Newton's 2. Lov, hastigheden som; hvor langt delt med hvor lang tid)

  1. Lav ovenstående model og sæt x ind i grafen, der viser måledata.


Umiddelbart er der to problemer:

Frekvensen af modellen er lidt for hurtig

Modellens amplitude bliver ikke mindre som tiden går.

Det første problem kan du løse ved at regulere (sænke) fjederkonstanten (k) en smule.

Løsningen af det andet problem kræver en ændring af modellen.

  1. Juster k, så modellens frekvens stemmer overens med den målte frekvens.


I den simple model har vi ikke taget hensyn til gnidningsmodstand inde i elastikken og luftmodstanden af koppen.


Gnidningsmodstanden kan beskrives som:   Fgnidning = -d. SIGN(v)

Luftmodstanden kan beskrives som:      Fluft = - c. v2 . SIGN(v)

SIGN(v) sikrer, at friktionskraften altid er modsat rettet bevægelsesretningen.


Kraften, der er brugt i den simple model, skal udvides med ovenstående to led:

Som startværdier kan du bruge: c = 0,03 N/(m/s)2 og d = 0,0015 N

  1. Sæt de to manglende led ind i din model.


  2. Leg med de tre konstanter og begyndelseshastigheden, indtil model og måling stemmer fuldstændig.


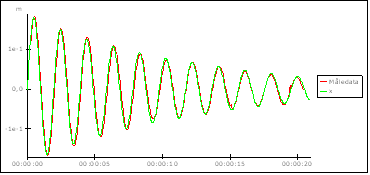
    I ovenstående simulering er brugt k = 1,265 N/m, c = 0,041 N/(m/s)2, d = 0,0021 N, v0 = 0,61 m/s.